Il triangolo di Tartaglia
Nella storia della matematica, soprattutto nei secoli passati, quando scambiarsi informazioni a grandi distanze era più difficile, si è assistito a un fenomeno curioso: diversi studiosi, indipendentemente l’uno dall’altro, arrivano a fare la stessa scoperta. Uno dei casi più evidenti è proprio quello che tratteremo in questo articolo; ad esempio questa figura, tratta da un manoscritto del 755 d.C., è il Meru Prastaara, la “scala sacra” per accedere al Monte Meru, il centro del mondo secondo la religione induista:
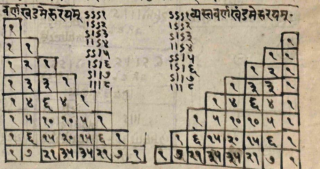Questa è una struttura numerica ideata dal matematico cinese Jia Xian nell’XI secolo d.C., che la usava come base di un metodo di calcolo delle radici quadrate, e che fu ripresa nel XIII secolo d.C. da Yang Hui, che ne approfondì le proprietà:
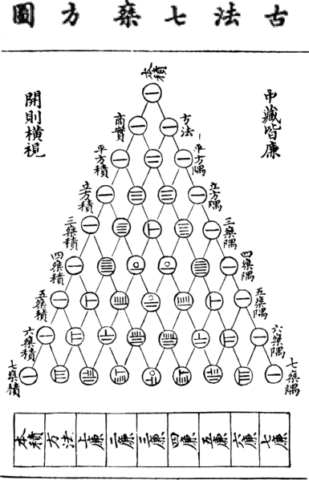
Infine, questo è il “triangolo aritmetico” del matematico francese Blaise Pascal, così come appare nel suo Traité du triangle arithmétique del 1654:
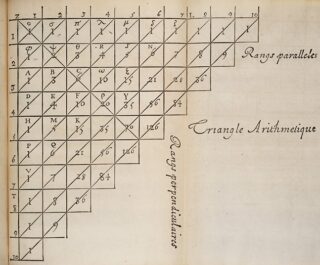
A parte le differenze di orientamento, e i diversi simboli usati per indicare i numeri che contiene, si tratta della stessa struttura; molti altri famosi matematici di tutto il mondo l’hanno studiata, ed è per questo che è nota con più nomi, di cui ne citiamo solo alcuni:
- I cinesi la conoscono come Triangolo di Jia Xian, o di Yang Hui;
- Nella maggior parte dei Paesi europei è nota come Triangolo di Pascal;
- In Iran si chiama Triangolo di Khayyam, da Omar Khayyam, matematico, poeta e astronomo persiano, che lo studiò nell’XI secolo d.C.;
- In Italia e Germania è noto come Triangolo di Tartaglia, da Niccolò Fontana detto Tartaglia, che lo descrisse nel suo General trattato di numeri et misure del 1556.
Cos’è il triangolo di Tartaglia?
Il triangolo di Tartaglia è una tabella triangolare con una sequenza di numeri differente su ogni riga.
La prima peculiarità di tale tabella è che l’n-esima riga presenta una sequenza di numeri con n elementi.
La sesta riga presenta sei elementi: 1, 5, 10, 10, 5, 1.
Il triangolo può idealmente proseguire all’infinito. Infatti ogni riga viene ricavata dalla precedente e il processo per costruire una nuova riga può essere ripetuto fino a una riga x-esima a piacere.
I numeri presenti sul triangolo possiedono molte interessanti proprietà. Prima di analizzarle, vediamo come costruire tale triangolo.
Come si costruisce il triangolo di Tartaglia?
Le prime due righe del triangolo hanno una struttura fissa. La prima riga sulla sommità del triangolo presenta solo il numero di partenza, ovvero 1.
| 1 |
Tale numero viene “copiato” agli estremi sinistro e destro della riga successiva. Poiché tale riga è la seconda e ci aspettiamo quindi solo due elementi, tali copie saranno gli unici numeri presenti. La tabella diventa quindi:
| 1 | |
| 1 | 1 |
Dalla terza riga in poi, il numero 1 viene sempre copiato agli estremi sinistro e destro. La terza riga, come detto, dovrà avere tre elementi. L’elemento che si trova nel centro viene calcolato sommando i numeri della riga precedente che si troveranno al di sopra di esso, in questo caso 1 + 1 = 2. La tabella diventa:
| 1 | |||||
| 1 | 1 | ||||
| 1 | 2 | 1 | |||
Per la quarta riga avremo quattro elementi. Il primo e l’ultimo, come già spiegato, saranno pari ad 1. Per gli altri numeri, dobbiamo addizionare le coppie di numeri consecutivi della riga precedente.
Per il numero in seconda posizione addizioniamo i numeri in prima e seconda posizione della riga precedente, in questo caso 1 + 2 = 3.
Per il numero in terza posizione addizioniamo i numeri in seconda e terza posizione della riga precedente, ovvero 2 + 1 = 3. Otteniamo che il triangolo di quattro righe è:
| 1 | |||||||
| 1 | 1 | ||||||
| 1 | 2 | 1 | |||||
| 1 | 3 | 3 | 1 | ||||
Con cinque righe:
| 1 | |||||||||
| 1 | 1 | ||||||||
| 1 | 2 | 1 | |||||||
| 1 | 3 | 3 | 4 | ||||||
| 1 | 4 | 6 | 4 | 1 | |||||
Infine, con sei righe:
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 | ||||||
Guarda il video per la costruzione del triangolo di Tartaglia fino a sei righe:
Triangolo di Tartaglia e potenza di un binomio
Un’importante proprietà del triangolo di Tartaglia è che i numeri dell’n + 1-esima riga corrispondono ai coefficienti dello sviluppo della n-esima potenza di un binomio.
La potenza di un binomio risulta in una somma di termini, ognuno contenente il prodotto dei due termini del binomio iniziale, con esponenti variabili man mano che la somma procede.
Per convenzione, si comincia dal primo termine del binomio elevato alla n-esima potenza, con l’esponente che diminuisce di 1 alla volta, fino a 0.
Il secondo termine del binomio, al contrario, ha un esponente che parte da 0 e cresce di 1 alla volta, fino all’esponente n.
Ciascuno di questi prodotti, contenenti il primo termine con esponente decrescente e il secondo con esponente crescente, avrà un coefficiente dato dalla n+1-esima riga del triangolo di Tartaglia e costituirà un termine dello sviluppo del binomio.
Notiamo inoltre che il binomio è elevato alla terza potenza. Questo ci dice che per individuare i coefficienti abbiamo bisogno della quarta riga del triangolo di Tartaglia:
| 1 | 3 | 3 | 1 |
Questo vuol dire che il primo termine dello sviluppo dovrà essere moltiplicato per 1, il secondo per 3, e così via.
- Al primo termine x del binomio di partenza diamo l’esponente 3, e l’esponente 0 ad y. Secondo il triangolo di Tartaglia, il coefficiente da moltiplicare sarà 1.
Otteniamo il termine1 \cdot x ^ 3 \cdot y ^ 0Semplificando tale termine e ricordando che il coefficiente 1 può diventare “invisibile” e che qualsiasi termine elevato a 0 è pari a 1, otteniamo che il primo termine dello sviluppo è:
1 \cdot x ^ 3 \cdot y ^ 0 = x ^ 3 - Svolgiamo lo stesso procedimento per il secondo termine. Dobbiamo abbassare l’esponente precedente di x di 1 e aumentare quello di y di 1 rispetto al termine precedente.
Ne segue che a x diamo l’esponente 2 e ad y l’esponente 1. Secondo il triangolo di Tartaglia il coefficiente sarà 3.
Otteniamo il termine1 \cdot 3 \cdot x ^ 2 \cdot y ^ 1Semplificando, otteniamo che il secondo termine è:
1 \cdot 3 \cdot x ^ 2 \cdot y ^ 1 = 3 x^2 y - Per il terzo termine reiteriamo il procedimento. Dobbiamo abbassare l’esponente precedente di x di 1 e aumentare quello di y di 1 rispetto al termine precedente.
Ne segue che a x diamo l’esponente 1 e ad y l’esponente 2. Secondo il triangolo di Tartaglia tale termine sarà moltiplicato per 3.
Otteniamo il termine3 \cdot x ^ 1 \cdot y ^ 2Semplificando, otteniamo che il terzo termine è:
3 \cdot x ^ 1 \cdot y \cdot 2 = 3 xy ^ 2 - Per l’ultimo termine, ancora una volta, dobbiamo abbassare l’esponente precedente di x di 1 e aumentare quello di y di 1 rispetto al termine precedente.
Ne segue che al primo termine x diamo l’esponente 0 e ad y l’esponente 3. Secondo il triangolo di Tartaglia tale termine sarà moltiplicato per 1.
Otteniamo il termine1 \cdot x ^ 0 \cdot y ^ 3Semplificando, otteniamo che il quarto termine è:
1 \cdot x ^ 0 \cdot y ^ 3 = y ^ 3
Si ha quindi che
Triangolo di Tartaglia e successione di Fibonacci
Un’altra interessante caratteristica del triangolo di Tartaglia è che le somme dei numeri sulle diagonali generano la famosa successione di Fibonacci.
Riportiamo qui i primi otto termini della successione di Fibonacci:
Ogni numero della successione viene calcolato come somma dei due numeri precedenti, partendo i primi due termini uguali ad 1.
Ad esempio il numero successivo a 21 risulta essere 13 + 21 = 34.
Riscriviamo ora qui il triangolo di Tartaglia per le prime sei righe:
Tracciamo una linea per ogni diagonale:
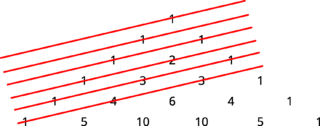
Se eseguiamo la somma di tutti i numeri attraversati da ogni diagonale otteniamo:
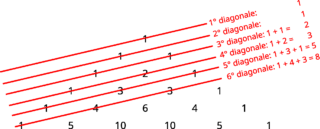
Ovvero i numeri 1, 1, 2, 3, 5, 8, che altro non sono che i primi sei numeri della successione di Fibonacci! Per calcolare l’n-esimo elemento della successione, è quindi sufficiente disegnare un triangolo di Tartaglia con n righe usando questo metodo.
Proprietà delle potenze
Un termine algebrico elevato a 0 è pari a 1.Binomio
Un binomio è un polinomio composto di soli due termini, di cui almeno uno dei due deve avere una variabile (cioè una lettera).2x - 5 è un binomio i cui due termini sono 2x e -5.
Potenza di un binomio
Un binomio elevato a un numero intero positivo viene definito come potenza di un binomio.(x + y) ^ 4 è il binomio x + y elevato alla quarta potenza.
