Pascal’s triangle
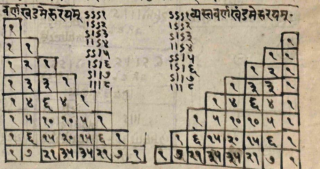
In the history of Mathematics, especially in past centuries, when exchanging information through large distances was more difficult, a curious phenomenon happened: different scientists, independently of one other, get to the same discovery. One of the most evident cases is just the one we’ll cover in this article; for example the following picture, taken from a manuscript of 755 A.C., is the Meru Prastaara, the “holy staircase” for accessing Mount Meru, the centre of the world according to Hindu religion:
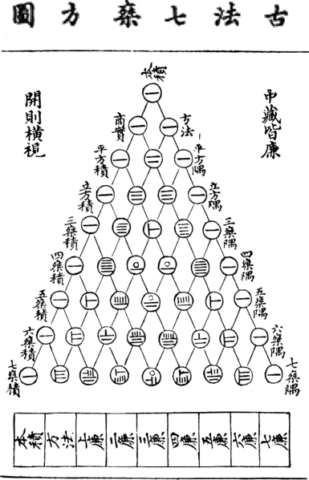
This is a numerical structure conceived by the Chinese mathematician Jia Xian in the 11th century A.C., who used it as the base of a method for computing square roots; the structure was taken up again in the 13th century A.C. by Yang Hui, who studied its properties in more detail:
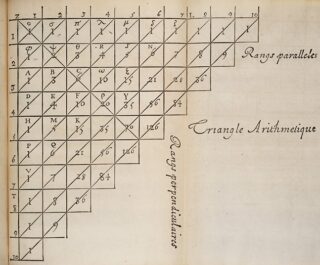
Finally, this is the “arithmetical triangle” by the French mathematician Blaise Pascal, as it appears in his Traité du triangle arithmétique of 1654:
A part from differences in orientation, and different symbols used for indicating the contained numbers, it’s the same structure; many other famous mathematician all over the world have studied it, and this is the reason why it’s referred to with several names, among which we’ll cite only some:
- Chinese people know it as Jia Xian’s triangle, or Yang Hui’s triangle;
- In most European countries it’s known as Pascal’s triangle;
- In Iran it’s called Khayyam’s triangle, from Omar Khayyam, a Persian mathematician, poet and astronomer, who studied it in the 11th century A.C.;
- In Italy and Germany it’s known as Tartaglia’s triangle, from Niccolò Fontana known as Tartaglia, who described it in his General trattato di numeri et misure of 1556.
What is Pascal’s triangle?
Pascal’s triangle is a triangular table with a different sequence of numbers on each row.
The first feature of this table is that the n-th row contains a sequence of numbers with n elements.
The sixth row contains six elements: 1, 5, 10, 10, 5, 1.
The triangle can ideally expand to infinity. In fact each row is obtained from the previous one and the process of building a new row can be repeated up to any row x you want.
The numbers in the triangle have many interesting properties. Before analyzing them, let’s see how to construct such a triangle.
How can Pascal’s triangle be constructed?
The first two rows of the triangle have a fixed structure. The first row on the summit of the triangle contains only the starting number, that is 1.
| 1 |
This number gets “copied” to the left and right ends of the next row. Since that row is the second one and so we expect only two elements, such copies will be its unique numbers. So the table becomes:
| 1 | |
| 1 | 1 |
From the third row on, the number 1 gets always copied to the left and right ends. The third row, as we said, will have three elements. The element in the middle is computed by summing up the numbers of the previous row that will be above it, in this case 1 + 1 = 2. The table becomes:
| 1 | |||||
| 1 | 1 | ||||
| 1 | 2 | 1 | |||
For the fourth row we’ll have four elements. The first and the last one, as we already explained, will be equal to 1. Concerning the other ones, we have to sum up the consecutive couples of numbers of the previous row.
For the number at second position we have to add the numbers at first and second position of the previous row, in this case 1 + 2 = 3.
For the number at third position we have to add the numbers at second and third position of the previous row, i.e. 2 + 1 = 3. We’ll obtain that the triangle of four rows is:
| 1 | |||||||
| 1 | 1 | ||||||
| 1 | 2 | 1 | |||||
| 1 | 3 | 3 | 1 | ||||
With five rows:
| 1 | |||||||||
| 1 | 1 | ||||||||
| 1 | 2 | 1 | |||||||
| 1 | 3 | 3 | 4 | ||||||
| 1 | 4 | 6 | 4 | 1 | |||||
Finally, with six rows:
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 | ||||||
Show the video about the construction of Pascal’s triangle up to the sixth row:
Pascal’s triangle and binomial power
An important property of Pascal’s triangle is that the numbers of the n + 1-th row correspond to the coefficients of the expansion of the n-th power of a binomial.
The power of a binomial results in a sum of terms, each containing the product of the two terms of the initial binomial, with exponents that change as the sum proceeds.
By convention, we begin from the first binomial term powered to the n-th power, with the exponent which decreases by 1 at time, up to 0.
The second binomial term, conversely, has an exponent which starts from 0 and increases by 1 at time, up to the exponent n.
Each of these products, containing the first term with a decreasing exponent and the second one with an increasing exponent, will have a coefficient given by the n+1-th row of Pascal’s triangle and it will constitute one term of the binomial expansion.
Moreover we see that the binomial is powered to three. This tells us that in order to find the coefficients we need the fourth row of Pascal’s triangle:
| 1 | 3 | 3 | 1 |
This means that the first term of the expansion has to be multiplied by 1, the second one by 3, and so on.
- We give the exponent 3 to the first term x of the initial binomial, and the exponent 0 to y. According to Pascal’s triangle, the coefficient to multiply by will be 1.
We obtain the term1 \cdot x ^ 3 \cdot y ^ 0Simplifying such term and remembering that the coefficient 1 cen become “invisible” and that any term powered to 0 is 1, we’ll obtain that the first term of the expansion is:
1 \cdot x ^ 3 \cdot y ^ 0 = x ^ 3 - Let’s follow the same procedure for the second term. We have to decrease the previous exponent of x by 1 and increase the one of y by 1 with respect to the previous term.
It follows that we give exponent 2 to x and exponent 1 to y. According to Pascal’s triangle the coefficient will be 3.
We obtain the term1 \cdot 3 \cdot x ^ 2 \cdot y ^ 1Simplifying, we’ll obtain that the second term is:
1 \cdot 3 \cdot x ^ 2 \cdot y ^ 1 = 3 x^2 y - For the third term we’ll repeat the procedure. We have to decrease the previous exponent of x by 1 and increase the one of y by 1 with respect to the previous term.
It follows that we give exponent 1 to x and exponent 2 to y. According to Pascal’s triangle such term will be multiplied by 3.
We’ll obtain the term3 \cdot x ^ 1 \cdot y ^ 2Simplifying, we’ll obtain that the third term is:
3 \cdot x ^ 1 \cdot y \cdot 2 = 3 xy ^ 2 - For the last term, again, we have to decrease the previous exponent of x by 1 and increase the one of y by 1 with respect to the previous term.
It follows that we give exponent 0 to the first term x and exponent 3 to y. According to Pascal’s triangle such term will be multiplied by 1.
We’ll obtain the term1 \cdot x ^ 0 \cdot y ^ 3Simplifying, we’ll obtain that the fourth term is:
1 \cdot x ^ 0 \cdot y ^ 3 = y ^ 3
So we’ll have that
Pascal’s triangle and Fibonacci sequence
Another interesting feature of Pascal’s triangle is that the sums of the numbers on diagonals generate the famous Fibonacci sequence.
We’ll write down here the first eight terms of Fibonacci sequence:
Each number of the sequence is computed as the sum of the two previous numbers, starting from the first two terms equal to 1.
For example the number which follows 21 turns out to be 13 + 21 = 34.
Now let’s write again here Pascal’s triangle up to the sixth row:
Let’s draw a line for each diagonal:
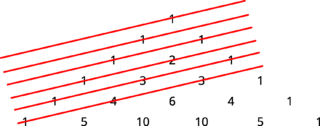
If we do the sum of all the numbers crossed by a diagonal we’ll obtain:
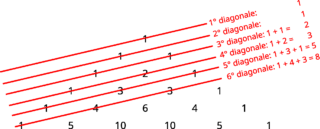
Namely, the numbers 1, 1, 2, 3, 5, 8, which are just the first six numbers of Fibonacci sequence! In order to compute the n-th element of the sequence, so, it’s sufficient to drae a Pascal’s triangle with n rows and use this method.
Properties of powers
An algebraic term powered to 0 is equal to 1.Binomial
A binomial is a polynomial made up of only two terms, of which at least one must have a variable (that is a letter).2x - 5 is a binomial in which the two terms are 2x and -5.
Binomial power
A binomial powered to a positive integer number is defined as binomial power.(x + y) ^ 4 is the binomial x + y powered to four.
